Uno dei passaggi chiave della data visualization è la scelta del metodo di rappresentazione dei dati raccolti. Utilizzare il giusto tipo di grafico consente di fornire una reportistica efficace e intuitiva; al contrario, adottarne uno sbagliato rischia di inficiare la validità di tutto il processo di raccolta e presentazione dei dati.
Per scegliere il metodo di rappresentazione migliore, è utile rifarsi alla tipologia di relazione che intercorre tra i dati da rappresentare: siamo di fronte a una serie temporale, ossia i valori assunti nel tempo da una certa variabile? Abbiamo un insieme di rilevazioni di cui vogliamo capire la distribuzione rispetto agli elementi considerati? Oppure abbiamo valori che rappresentano le diverse porzioni di un insieme?
Il libro Show Me the Numbers, di Stephen Few (ed. Analytics Press, Burlingame, 2012), elenca sette tipi di relazione. In un articolo precedente abbiamo visto i primi tre (serie temporali, ranking, parti per il tutto).
In questo, completiamo la nostra panoramica analizzando le altre quattro possibili relazioni, ovvero deviazioni, distribuzioni, correlazioni e rappresentazioni geospaziali.
Le deviazioni
A volte l’obiettivo di un grafico non è mostrare semplicemente l’andamento dei dati, ma evidenziare piuttosto in che modo una o più serie di valori differiscono rispetto a una serie presa come benchmark di riferimento. In questo caso si parla di grafici di analisi delle deviazioni.
Ad esempio l’andamento di costi o ricavi a consuntivo, rispetto a quanto messo a budget, i lead generati dalle azioni di vendita rispetto alle previsioni e così via.
Il focus non è quindi sulla grandezza principale, quanto piuttosto sul suo scostamento.
Come rappresentare graficamente le deviazioni
Per evidenziare queste differenze si possono seguire diverse strade.
- La prima (e più comune) è utilizzare degli istogrammi opportunamente rivisti: ad esempio affiancando le coppie valore attuale / valore di riferimento per ogni grandezza analizzata.
- Questo grafico, sicuramente valido, è forse fin troppo ricco di informazioni. Quando si vuole evidenziare solo lo scostamento senza mostrare ciò che lo ha generato, lo si può indicare come valore unico sempre su un istogramma.
- O ancora, le coppie valore attuale / valore di riferimento possono essere sovrapposte, utilizzando una barra più sottile dell’altra: in questo modo il grafico risulta più compatto e di facile lettura.
Ciascuna scelta, pur utilizzando grafici a barre, evidenzierà aspetti diversi del fenomeno.
In altri casi potremmo però voler dare informazioni ancora più complete; in particolare, potremmo voler guidare il lettore in una maggiore comprensione del dato dello scostamento facendogli sapere se il risultato effettivo si trova nell’ambito di un risultato buono, accettabile o negativo.
Ad esempio: potremmo non aver raggiunto l’ambizioso budget previsto, ma vorremmo far sapere al destinatario del report che ci troviamo comunque di fronte a un livello di incassi accettabile; o, al contrario, evidenziare che siamo di fronte a un risultato decisamente negativo.
In questi casi si può ricorrere al bullet graph (ne abbiamo parlato a lungo qui). Per costruirlo, le barre del nostro istogramma verranno quindi disposte su uno sfondo colorato con diversi gradienti di colore che, come un termometro, ci mostreranno in che area di accettabilità del risultato ci troviamo.

Questo sistema permette una lettura guidata dei dati. La definizione di risultato insufficiente, buono o ottimo ricade quindi sull’analista.
Le distribuzioni
Si ricorre a un grafico di distribuzione ogni volta che si vuole evidenziare come i valori di una serie di dati disaggregati sono distribuiti nelle unità statistiche che compongono l’insieme oggetto di analisi.
Ad esempio:
- Come si distribuisce la variabile “altezza” in un certo insieme di individui?
- Come si distribuiscono i fatturati delle aziende di un certo settore?
- E i gol segnati dai giocatori durante il campionato?
Rappresentare la distribuzione dei valori significa evidenziare, quindi, quali sono i valori ricorrenti o quelli estremi, o ancora qual è l’intervallo di valore in cui ricade la maggior parte delle variabili. In particolare si parla di moda (il valore più frequente), media (ovvero la media aritmetica), mediana (il valore centrale tra i dati numerici raccolti).
Come rappresentare graficamente le distribuzioni
Il primo passo per scegliere il tipo di rappresentazione da utilizzare è capire se analizzare separatamente tutti i valori, o se raggrupparli in intervalli, detti anche “bin”.
Ad esempio, se vogliamo rappresentare le altezze degli alunni di una certa classe, possiamo scegliere se basarci sull’altezza effettiva oppure se creare intervalli da 10 cm ciascuno. Generalmente la scelta dipende dalla quantità di rilevazioni, oltre che dagli scopi delle analisi.
Una volta scelto se rappresentare ogni singolo dato o se raggrupparli in bin differenti, potremo ricorrere a istogrammi o curve di distribuzione.
Gli istogrammi si prestano a rappresentare un numero di dati (o di bin) minore. In questo caso si mettono in evidenza soprattutto gli intervalli in cui si verifica la maggior parte degli eventi. Le curve di distribuzione, invece, evidenziano soprattutto come gli stessi dati si distribuiscono lungo la serie.
Le curve di distribuzione utilizzate normalmente sono le classiche curve di Gauss e, su campioni statisticamente rilevanti, tendono ad assumere delle forme tipiche. Quella più celebre è la classica curva “a campana”, che si ha quando l’asse di simmetria si ha nel punto in cui coincidono media, mediana e moda della distribuzione. Altre volte, invece, otteniamo curve asimmetriche nelle quali questi valori sono situati in punti diversi del grafico.
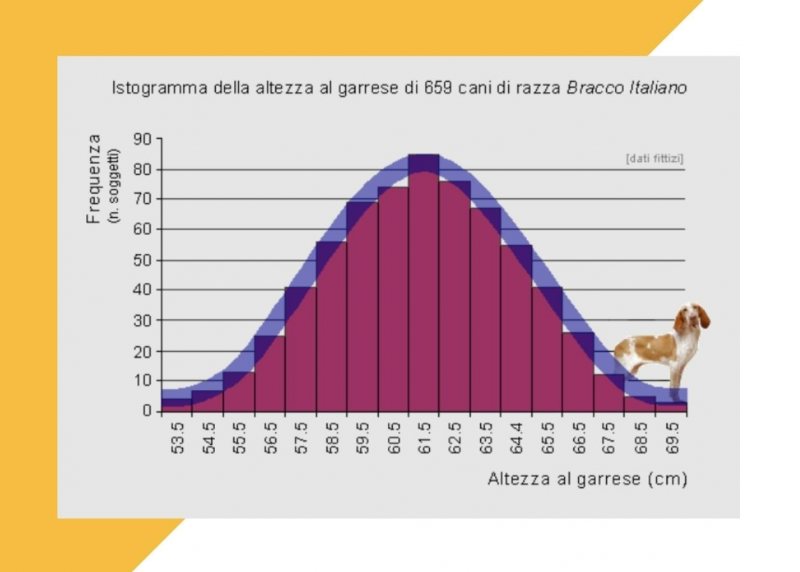
Fonte: www.quadernodiepidemiologia.it/
Un metodo di rappresentazione più compatto a livello visivo, ma decisamente meno comune, è dato dai grafici strip plot.
In questo caso i valori misurati vengono rappresentati su un unico asse cartesiano; l’utilizzo del colore aiuta a evidenziare le aree del grafico dove c’è una maggiore concentrazione di rilevazioni.
In alcuni casi particolari potremmo voler evidenziare non tanto i valori misurati, ma le loro deviazioni rispetto a moda, mediana e media.
In questi casi si ricorre ai grafici chiamati box and whiskers, ovvero scatole e baffi.
La logica di base del box and whiskers ricorda quella dei grafici strip plot: rappresentiamo i dati lungo un unico asse (stavolta verticale), utilizzando però non dei cerchi ma delle “scatole” di diverso colore che rappresentano visivamente i principali percentili.
Sempre su quest’asse, poi, segniamo delle brevi linee orizzontali (i “baffi” richiamati nel nome del grafico) per evidenziare invece i limiti entro i quali si trovano i dati statisticamente rilevanti.
Anche se i grafici box and whisker sono meno comuni, risultano comunque molto intuitivi alla lettura.
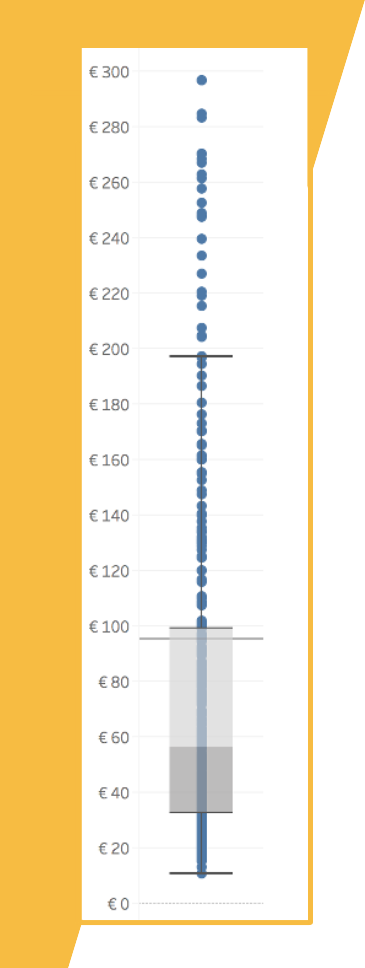
Fonte: libro Fabio Piccigallo – Data Storytelling
Le correlazioni
La caratteristica fondamentale dei grafici di correlazione è che non prendono in esame un unico set di dati, ma cercano anzi di evidenziare la presenza (o meno) di correlazione tra due diversi fenomeni. Solo se il grafico dimostra l’evidenza di una correlazione si potrà poi ricercarne la causa e la natura.
Vale la pena, a questo proposito, ricordare che una correlazione non sempre indica un rapporto di causalità tra due variabili (né una qualche relazione tout-court).
In particolare, potremmo avere:
- correlazioni di causa-effetto (se varia x, allora varierà anche y)
- correlazioni non significative, ovvero quando i due fenomeni sono, in realtà, dipendenti entrambi da un terzo fattore (x e y dipendono entrambe da z. Quando z varia, anche x e y variano ma senza che siano in relazione diretta tra loro).
- correlazioni spurie, o casuali (x e y mostrano effettivamente di muoversi in modo coerente, ma non esiste alcuna spiegazione razionale per questa correlazione).
Quando ci troviamo di fronte a correlazioni di causa-effetto, si può costruire un modello matematico che mostra come y varierà in relazione a x.
La correlazione più comune è la correlazione lineare, che è espressa dalla formula y=ax+b
Come rappresentare graficamente una correlazione?
Per rappresentare le correlazioni si ricorre, generalmente, allo scatterplot.
Lo scatterplot permette di aggiungere virtualmente una dimensione alla rappresentazione visiva classica, così da rendere facilmente individuabili le eventuali relazioni tra gli elementi analizzati.
Immaginiamo, ad esempio, di voler definire se c’è un nesso tra la mortalità infantile e reddito medio pro-capite nei diversi paesi del mondo. Entrambi i valori verranno posti su un asse cartesiano, che mostrerà in modo intuitivo se vale la pena ricercare un modello di correlazione lineare tra i due valori.
La correlazione in questo caso sembra essere presente e mostra effettivamente che a basso reddito pro-capite corrispondono livelli di mortalità infantile maggiore (come era facile immaginare). Una linea di tendenza opportunamente disegnata permetterà poi di evidenziare questa relazione.
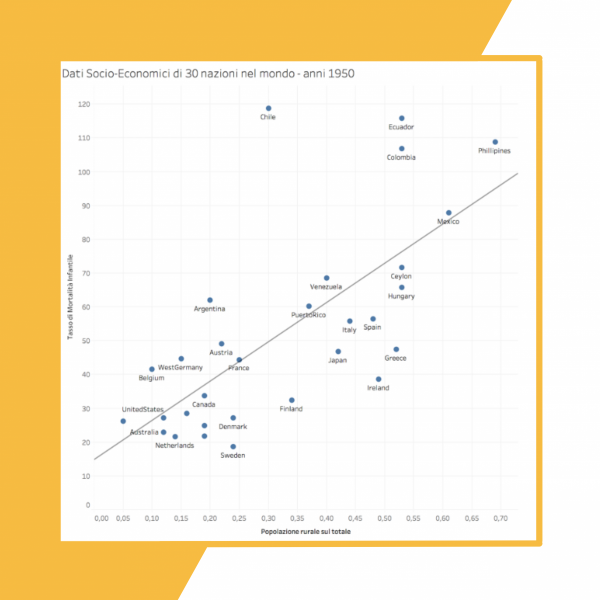
Fonte: libro Fabio Piccigallo – Data Storytelling
Questo tipo di grafico non è, ovviamente, la sola possibilità. Come sempre, una rappresentazione diversa potrà anzi evidenziare altri aspetti del fenomeno analizzato.
Riprendendo lo stesso esempio, un’altra possibilità è il ricorso a due grafici a barre affiancati: paese per paese, avremo una barra che evidenzia il reddito pro-capite e l’altra il livello di mortalità infantile.
Avendo l’accortezza di ordinare il primo set di valori dal più grande al più piccolo, sarà facile verificare se anche il secondo ha un andamento simile (oppure se ne ha uno inverso, dimostrando anche in questo caso la presenza di una correlazione).
Le rappresentazioni geospaziali
L’ultimo tipo di relazione tra dati investigato da Few è costituito dalle rappresentazioni geospaziali. Queste si riferiscono a quegli insiemi di dati in cui gli elementi nominali sono di carattere geografico (Paesi, città, regioni, continenti, province…).
Qual è il livello di occupazione in ogni regione italiana? E il PIL pro capite dei diversi Paesi dell’Unione Europea? O la suddivisione, per ogni nazione, del PIL tra i settori economici principali (agricoltura, industria, terziario)?
In tutti questi casi si sceglie spesso un tipo di rappresentazione che evidenzierà quanto voluto direttamente su una cartina geografica, mostrando quindi ogni Paese (o ogni città, regione, ecc) nella sua esatta collocazione spaziale.
Rappresentare i dati in relazione geospaziale
Per individuare la forma di rappresentazione geospaziale migliore, è utile separare due possibili casi e capire in quale di essi ci stiamo muovendo. Avremo rappresentazioni diverse, quindi:
- quando occorre rappresentare una sola metrica (ad esempio, il PIL pro capite di un insieme di nazioni)
- quando occorre rappresentare un sistema di dati più complesso (ad esempio, come il PIL pro capite si suddivide tra i diversi settori economici nelle varie nazioni considerate).
Nel primo caso, il più semplice, di solito ci si appoggia a una convenzione grafica che evidenzia in modo intuitivo un peso maggiore o minore della variabile considerata in ciascun Paese: ad esempio, dei cerchi di diversa dimensione apposti sulla cartina geografica, in corrispondenza di ciascuno stato o regione, oppure una colorazione diversa, più scura laddove il valore da rappresentare è più alto.
Le rappresentazioni di questo tipo permettono una visualizzazione molto intuitiva del fenomeno in oggetto e sono, infatti, molto comuni. Spesso vengono integrate con delle etichette con i dati numerici per renderle più precise ed esaustive.
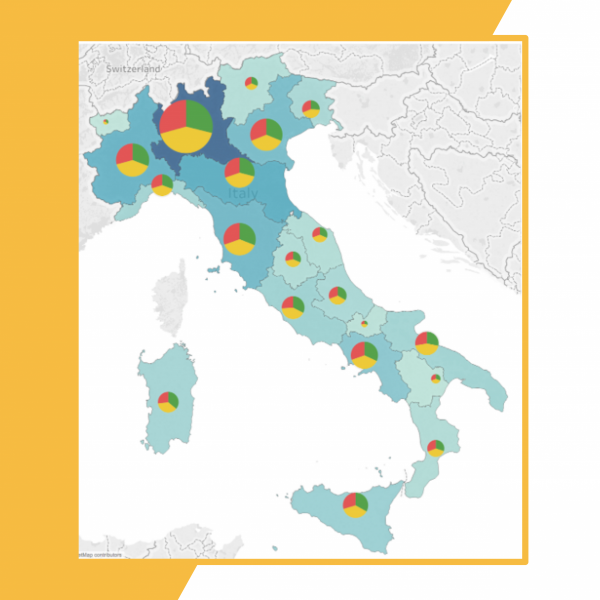
Fonte: libro Fabio Piccigallo – Data Storytelling
Nel secondo caso, invece, di solito si provvede a posizionare su ogni singolo stato o regione un grafico di piccole dimensioni che mostra il set di dati da rappresentare per quell’area geografica.
Ad esempio, un grafico a torta su ogni paese preso in esame per mostrare la suddivisione del PIL tra i diversi settori economici, o un istogramma.
Devono essere ovviamente grafici semplici, di lettura molto intuitiva e che possono essere compresi anche se visualizzati in piccole dimensioni. Elementi complessi sarebbero di lettura faticosa e porterebbero a un inutile overload informativo
In conclusione…
Spesso, trovandoci davanti a un set di dati, abbiamo qualche momento di difficoltà nell’individuare il grafico migliore per visualizzarli. Il primo passo deve sempre essere quello di partire dall’individuazione della relazione esistente tra i dati che abbiamo davanti. Mettere a fuoco questa relazione ci consentirà di individuare più facilmente il grafico più appropriato. Noi to abbiamo fornito una guida di massima, ma ci auguriamo che questa disamina delle possibili rappresentazioni grafiche sia prima di tutto un invito alla riflessione, per non fermarti al tipo di grafico più comune ma ragionare in modo approfondito sul tipo di dati da rappresentare e su cosa vuoi evidenziare.
In questo modo potrai ottenere grafiche e reportistiche migliori, più efficaci e fruibili, fornendo un servizio prezioso a chi, sulla base di quei dati, dovrà prendere decisioni strategiche per l’azienda.









