Come abbiamo già visto in questo articolo del nostro blog, per rappresentare al meglio i dati occorre capire in che rapporto sono, tra di loro, le grandezze che si vogliono rappresentare. Siamo di fronte all’evolversi di un certo fenomeno nel tempo? Oppure stiamo cercando una correlazione tra eventi? 

Capire il tipo di relazione tra dati è, quindi, il primo passo per poter scegliere il tipo di visualizzazione capace di rappresentarli al meglio. Una fotografia efficace e completa di tutti i tipi di relazioni che possono intercorrere tra i dati ci è stata data da Stephen Few nel tuo libro Show Me the Numbers (ed. Analytics Press, Burlingame, 2012) e di cui abbiamo già avuto modo di parlare. 

In questo articolo vedremo insieme come visualizzare al meglio le prime tre relazioni individuate da Few, ovvero:

• Serie temporali
• Ranking 
• Parti per il tutto

Le serie temporali

Ci troviamo di fronte a serie temporali ogni volta in cui si vuole analizzare il modo in cui una o più metriche si modificano nel corso del tempo: ad esempio, il fatturato mensile di un’azienda oppure l’incremento/decremento di popolazione, anno dopo anno, in una data nazione, o ancora le calorie assunte giornalmente durante un periodo di dieta. 

Questo è probabilmente il tipo di relazione di dati più semplice e di immediata comprensione, tanto che esiste un ampio vocabolario per descrivere questi andamenti: si parla di incrementi, diminuzioni, fluttuazioni, tendenze… tutti termini di utilizzo comune e comprensibili ai più.

I sistemi di rappresentazione delle serie temporali

Per convenzione, le serie temporali vengono rappresentate su un piano cartesiano. Il tempo è rappresentato dall’asse delle ascisse e si muove da sinistra a destra; l’asse delle ordinate rappresenta invece il valore rappresentato. 

Proprio perché sono grafici molto comuni, utilizzare sistemi di rappresentazione diversa sarebbe controproducente: nella migliore delle ipotesi richiederebbe uno sforzo cognitivo notevole da parte del lettore, nella peggiore risulterebbero incomprensibili. 

Ci possono essere però delle eccezioni: questo tipo di rappresentazione classica, infatti, si riferisce a tutti quei casi in cui il tempo è trattato come una variabile continua, mentre si rivela molto meno adatto a rappresentare il tempo quando è trattato, invece, come una variabile discreta. Prima di continuare sarà utile, quindi, capire questa differenza.

Tempo continuo, tempo discreto (o dimensionale)

Una variabile continua è una variabile che si riferisce a una progressione infinita, misurata secondo intervalli o rapporti prestabiliti. Nel caso del tempo possono essere i giorni che scorrono, o i mesi che passano, o gli anni: tutte queste sono senza dubbio variabili continue.

Il tempo “continuo” è quindi il tempo che scorre e che noi ci preoccupiamo di misurare.  

A livello di rappresentazione, come abbiamo già detto si ricorre di solito al piano cartesiano. Sull’asse delle ascisse per ogni anno (o giorno, o mese, o ora…) che passa si aggiunge una tacchetta alla nostra scala, e così via fino potenzialmente all’infinito.

E, mentre sulle ascisse scorre il tempo, sulle ordinate potremo segnare come si muove la variabile che stiamo rappresentando.

Anche se i dati saranno quasi sicuramente puntuali (ad esempio il fatturato di ogni mese), di solito si sceglie di utilizzare una linea continua per rappresentarli. La linea consente infatti di individuare meglio i trend presenti nel grafico. 

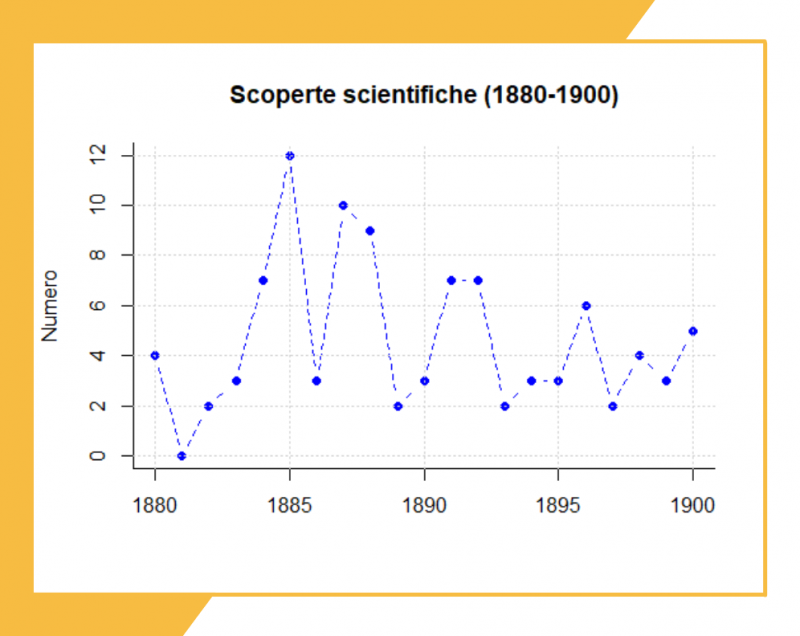
Si possono, ovviamente, scegliere altri metodi di rappresentazione: potremmo ad esempio utilizzare una serie di barre al posto della linea continua, e così facendo evidenzieremmo i singoli valori a discapito del trend complessivo. Come sempre, la scelta della rappresentazione dipende da ciò che si vuole evidenziare agli occhi del lettore.

A questo punto ci si può chiedere come faccia il tempo, invece, ad essere una variabile discreta. Una variabile quantitativa è detta discreta quando dipende da un processo di enumerazione ed è quindi finita.  

Per capirci, pensiamo al modo in cui suddividiamo il tempo: le 24 ore del giorno, i 7 giorni della settimana, i 12 mesi dell’anno rappresentano tutti esempi di variabili temporali discrete.

I dati da rappresentare potrebbero essere, allora, il numero di accessi a sito web in una certa ora del giorno, oppure gli incidenti automobilistici nei diversi giorni della settimana.

Immaginiamo di rappresentare anche questo tipo di dati su un asse cartesiano. Sicuramente è una scelta sempre possibile, ma si rischia di perdere completamente il senso di ciclicità di queste grandezze. In linea generale consigliamo, quindi, di ricorrere al sistema delle coordinate polari, che risulta più facile da decodificare proprio perché mostra la ciclicità dei valori. Si utilizzerà quindi, nella maggior parte dei casi, un grafico radar (per consigli su come usarlo al meglio, c’è questo articolo del nostro blog che potrebbe tornarti utile).

Il ranking

Ranking è un termine inglese che in italiano possiamo tradurre come “classifica”. Quando la relazione tra dati è di ranking, significa che stiamo assegnando a ciascuna categoria un diverso valore, così da poterle ordinare da quello più basso a quello più alto, o viceversa.

Anche qui gli esempi sono infiniti: quante medaglie ha guadagnato ciascuna nazione alle olimpiadi (e chi ne ha vinte di più)? Quante matricole si sono iscritte alle diverse università italiane (e quali hanno quindi raccolto più iscrizioni)? Quanto è costato in manutenzione ogni veicolo del nostro parco auto nel corso dell’ultimo anno (e quali veicoli sono costati meno)? E così via.

Rappresentare il ranking in modo efficace

Proprio come nel caso dei grafici temporali, anche qui siamo di fronte a modalità di visualizzazione molto comuni. 

Generalmente si ricorre a un grafico a barre orizzontali: basta un semplice elenco delle categorie e accanto una barra che ne rappresenta il valore, disegnata seguendo la stessa scala. Per aumentare la leggibilità consigliamo di ordinare le variabili (generalmente dalla “migliore” alla “peggiore”) in modo che la classifica sia evidente a colpo d’occhio.

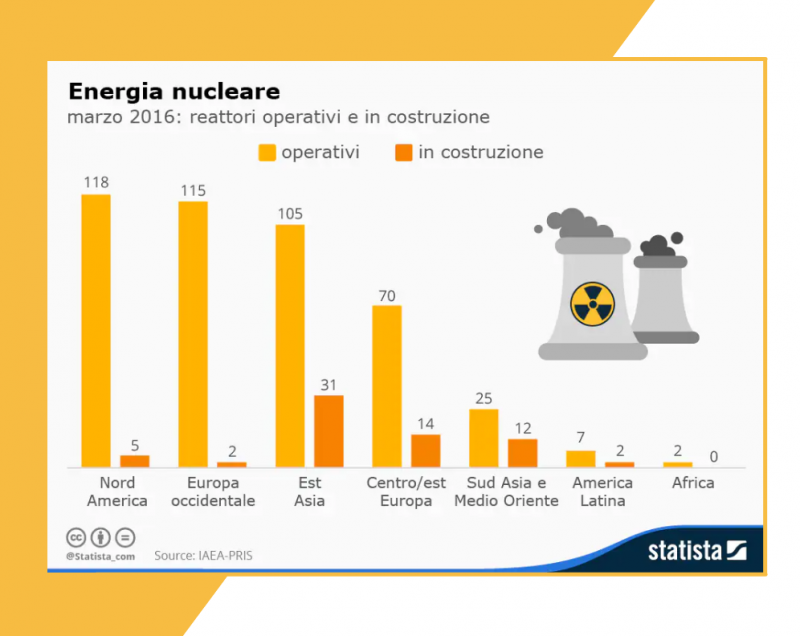
Le parti per il tutto

Si parla di “parti per il tutto” quando ci troviamo di fronte a singoli dati che, nel loro complesso, vanno a comporre una totalità. La relazione che intercorre tra loro è quindi quella di essere una parte di un un unico insieme. Ad esempio, i dati da rappresentare potrebbero essere i fatturati delle singole categorie di prodotto in un e-commerce (tutti insieme, questi dati formano il fatturato totale), o ancora le popolazioni delle diverse regioni italiane che, insieme, formano il totale delle popolazione nazionale. 

Proprio perché si vuole evidenziare la relazione rispetto al totale, e cioè quanto ognuna di queste parti “pesa” sul totale, spesso si ricorre a dati espressi in forma percentuale anziché assoluta. Fatto 100 il fatturato totale nell’anno, quindi, il grafico ne evidenzierà la composizione rivelando, ad esempio, quanta parte deriva dalla vendita di articoli di abbigliamento, quanta dalla vendita di accessori, quanta da prodotti per la casa, eccetera.

A ben vedere, la relazione che vogliamo mettere in evidenza è quindi duplice: ogni variabile verrà valutata sia per il suo peso rispetto al totale, sia rispetto alle altre variabili che compongono l’insieme. 

Rappresentare le parti per il tutto: il grafico a torta

La scelta più ovvia per il tipo di rappresentazione “parti per il tutto” è il grafico a torta, che sicuramente ha un’immediatezza visiva e una semplicità di decodifica che lo rendono molto, molto comune. Così comune che spesso non si pensa, invece, a quante trappole nasconde in certi casi questo tipo di rappresentazione… (qui abbiamo parlato del perché i grafici a torta andrebbero evitati come la morte!)

In primo luogo, confrontare valori simili non è sempre agevole; l’uso di colori diversi per evidenziare i diversi spicchi della torta, poi, potrebbe falsare la percezione, poiché l’occhio tende a percepire come più grandi le aree di colore chiaro rispetto a quanto siano in realtà.

Un altro problema si ha quando i valori da mostrare sono molti, perché all’interno del grafico si crea un affollamento visivo che peggiora la percezione. Infine, la recente moda di mostrare il grafico non come un cerchio perfetto visto dall’alto, ma in prospettiva, aumenta il rischio di distorsioni nella percezione dei valori rappresentati (ricorda che i grafici in 3D andrebbero sempre evitati!)

 

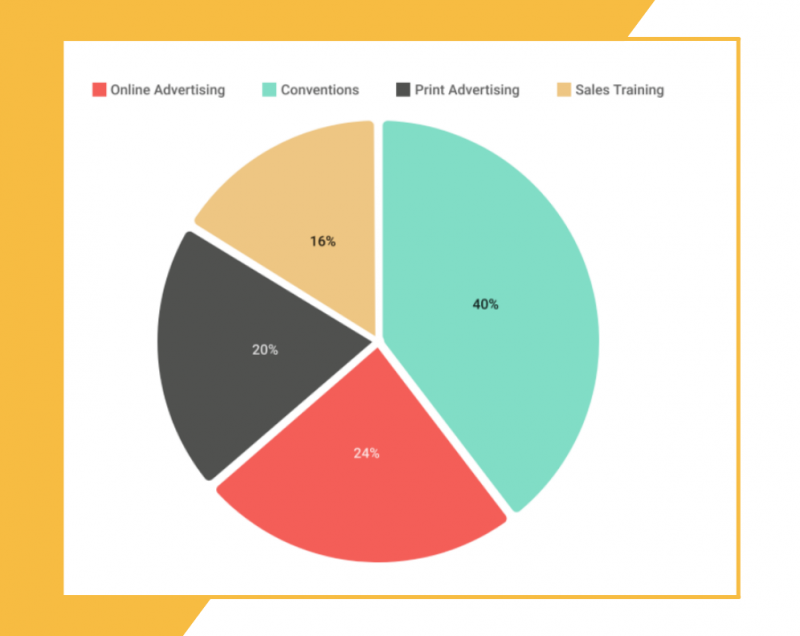
Si tratta quindi di un buon grafico, ma non sempre della scelta migliore. 

Ecco qualche trucco per rendere migliore questo tipo di rappresentazione:

• utilizza colori diversi per i diversi spicchi aiuta a identificarli visivamente, ma fai attenzione a che non siano colori troppo dissimili o che alterino la percezione (es. tutti colori pastello e poi un nero o un rosso acceso che attraggono troppo l’attenzione);
• aggiungi delle etichette con i valori numerici, che possono semplificare notevolmente il confronto;
• ricorda che le proporzioni tra i diversi spicchi diventano più semplici da comprendere se questi vengono ordinati a seconda della loro ampiezza.

Nonostante queste attenzioni, comunque, il grafico a torta non è una soluzione universale per il tipo di relazione “parti per il tutto”. 

In particolare, esistono alcune alternative che possono rivelarsi molto utili o quando dobbiamo rappresentare un numero abbastanza alto di variabili, oppure quando vogliamo evidenziare, oltre alle proporzioni, il modo in cui queste evolvono nel tempo.

Il grafico a barre

L’utilizzo di barre orizzontali o verticali può aiutarci, in particolare, quando abbiamo molte variabili da mostrare. Suddividiamo una barra in aree di colore diverso e di ampiezza proporzionale al valore da rappresentare: in questo modo possiamo mostrare in modo più chiaro la presenza di tante diverse componenti.

Il grafico a barre si rivela molto utile anche quando vogliamo mostrare come la composizione di un insieme varia nel corso del tempo. Le diverse barre (tutte di uguale altezza e larghezza e suddivise in aree di diverso colore, come già visto) vengono disposte lungo un piano cartesiano, convenzionalmente usato per la rappresentazione del tempo come variabile continua. In questo modo, i trend di aumento o diminuzione delle diverse componenti rispetto al totale diventano immediatamente evidenti per l’osservatore.

Il grafico di Pareto

Torniamo alle due esigenze fondamentali che incontriamo quando ci troviamo di fronte a grandezze che sono parte di un insieme: mostrare la relazione che intercorre tra loro e quella di ogni singola parte con l’insieme stesso.

Il diagramma di Pareto (puoi vederlo meglio qui) risolve il problema della doppia rappresentazione ricorrendo a due diversi tipi di segno grafico, da utilizzare nello stesso diagramma.

Nel diagramma di Pareto abbiamo infatti un grafico a barre verticali che rappresenta i dati assoluti delle categorie in ordine decrescente. Ad esse, poi, viene associata una curva che corrisponde al valore percentuale cumulato delle incidenze di ogni valore rappresentato nel grafico a barre. Diventa facile, così, capire a colpo d’occhio il contributo che le categorie più importanti danno al raggiungimento del valore complessivo.

Parti per il tutto: casi particolari

Le rappresentazioni viste finora per le relazioni tra dati di “parti per il tutto” si basano, sostanzialmente, sulla presenza di variabili che sono della stessa tipologia. 

Ma le cose possono essere molto più complicate di così: ci potrebbe ad esempio essere necessità di rappresentare non un semplice insieme di dati, ma anche il modo in cui questi si raggruppano tra di loro, formando di fatto dei sottoinsiemi o trovandosi in altre forme di relazione l’uno con l’altro.

Un esempio classico è la rappresentazione grafica di un conto economico sintetizzato. L’insieme è dato dai ricavi; togliendo i costi di produzione si arriva al margine lordo industriale; sottraendo ancora costi di marketing e costi di distribuzione, si arriva al margine lordo operativo, e via discorrendo.

Questo genere di scomposizione può essere rappresentata con un waterfall chart, o grafico a cascata: in esso vengono via via evidenziate le quantità da sottrarre all’insieme per arrivare, alla fine, al margine lordo industriale – o al valore ultimo dei dati che stiamo visualizzando. I valori positivi vengono rappresentati sull’asse delle ascisse, quelli dei costi vengono invece mostrati come capovolti, allo stesso livello dell’ultimo subtotale.

Puoi vederne un esempio qui.

In conclusione…

Termina qui il nostro esame dei primi tre tipi di relazioni tra dati individuati da Stephen Few. Nel prossimo articolo parleremo di deviazioni, distribuzioni, correlazioni e relazioni geografiche, così da avere una panoramica completa dei tipi di grafico che meglio si adattano a rappresentare ciascun tipo di relazione. Continua a seguirci per non perderti il prossimo post!